Czy warto wyłączać ogrzewanie na noc? Ile można zaoszczędzić na okresowym wyłączaniu ogrzewania?
 Do tego problemu wracałem myślami wielokrotnie i ciągle jakoś nie mogłem się zebrać, by sumiennie go zgłębić. Intuicyjnie wiadomo, że taniej jest nie grzać przez pewien czas, niż grzać nieustannie, ale nie chodzi sam o fakt. Chodzi raczej o to, ile konkretnie można zaoszczędzić?
Do tego problemu wracałem myślami wielokrotnie i ciągle jakoś nie mogłem się zebrać, by sumiennie go zgłębić. Intuicyjnie wiadomo, że taniej jest nie grzać przez pewien czas, niż grzać nieustannie, ale nie chodzi sam o fakt. Chodzi raczej o to, ile konkretnie można zaoszczędzić?
Dzisiaj nadszedł wreszcie czas by rozprawić się z problemem.
Poszukiwania, poszukiwania …
Oczywiście rzecz wymagała odpowiedniego przygotowania. Przyznaję, że znowu (podobnie jak przy tworzeniu kalkulatora emerytalnego) nie znalazłem w internecie niczego, co w sposób dostatecznie precyzyjny, a jednocześnie prosty i czytelny rozwiązywało by problem. Większość to lanie wody, w stylu „koszty mogą spaść od 5 do 12 %”, albo „lepiej wyłączać, bo będzie taniej”, lub wręcz odwrotnie „lepiej nie wyłączać, bo jak się wyłączy, to ponowne podgrzanie wyjdzie drożej”.
Chaos informacyjny wymieszany z reklamami produktów, pogłębiającymi jedynie ten chaos.
Cóż było robić? Trzeba było zacząć drążyć.
Kluczem do rozwiązania naszej zagadki będzie wiedza zdobyta przez nas we wpisie: Jak policzyć straty ciepła uciekającego z mieszkania
UWAGA, ważne!
Kontynuacja czytania tego wpisu ma sens jedynie po zapoznaniu się z poprzednim: Jak policzyć straty ciepła uciekającego z mieszkania. Jeżeli nie czytałeś tego wpisu, przeczytaj go najpierw! Koniecznie!
Strumień ciepła uciekający z mieszkania
Do oceny opłacalności wyłączania ogrzewania w nocy, niezbędny będzie nam strumień ciepła, który liczyliśmy we wpisie: Jak policzyć straty ciepła uciekającego z mieszkania. Wprowadzimy tu jednak pewną modyfikację, która zdecydowanie ułatwi nam życie.
Przypomnijmy sobie najpierw zależność, dzięki której obliczyliśmy strumień ciepła. Jeżeli poniższy wzór budzi Twoje obrzydzenie, to nie martw się. Nie musisz go znać !!! Poniżej podaję krok po kroku prosty przepis, według którego policzysz wszystko bez większego kłopotu.
gdzie:
U – współczynnik przenikania ciepła przegrody [W/(m2*K)]
S – powierzchnia przegrody [m2]
Tw – temperatura wewnątrz mieszkania [K]
Tz – temperatura otoczenia na zewnątrz [K]
Zrobimy drobne przekształcenie. Podzielimy obie strony równania przez (Tw – Tz).
Otrzymamy:
Przyjmijmy jednocześnie, że (Tw – Tz) = 1, czyli ze różnica temperatury pomiędzy wnętrzem mieszkania, a otoczeniem zewnętrznym to 1 K. Otrzymamy:
Q/1 oznaczmy nowym symbolem: q
otrzymamy:
Otrzymaliśmy w ten sposób charakterystyczną dla naszego mieszkania jednostkową utratę ciepła q, czyli ilość ciepła jaka ucieka z naszego mieszkania przy jednostkowej różnicy temperatur (wewnętrznej i zewnętrznej). Innymi słowy, nasze mieszkanie traci taką ilość ciepła na każdy stopień różnicy temperatur między temperaturą wewnątrz i na zewnątrz.
Jeżeli różnica temperatur wyniesie 3 stopnie, to strumień ciepła uciekającego z mieszkania wyniesie:
![]()
a jeżeli różnica wyniesie 10 stopni, to strumień ciepła wyniesie
![]()
W praktyce na całkowity jednostkowy strumień ciepła (q) składa się sumy jednostkowych strumieni, które przenikają przez: ściany, okna, podłogę, sufit i drzwi.
Żeby go policzyć, musimy policzyć i zsumować wszystkie strumienie składowe.
Policzmy więc jednostkowe strumienie składowe dla mojego mieszkania.
Okna
Powierzchnia okien: S = 13,5 m2
Współczynnik przenikania ciepła dla okien: U = 1,3 W/(m2*K)
q = U * s = 13,5 * 1,3 = 17,55 [W/K]
Drzwi wejściowe
Drzwi wejściowe w moim mieszkaniu nie wychodzą bezpośrednio na zewnątrz. Wychodzą na ogrzewaną klatkę schodową. Ewentualne straty ciepła w tym przypadku mogę pominąć.
q = 0 [W/K]
Ściany
Trzy ściany są ścianami zewnętrznymi, a jedna graniczy z sąsiadem. Przyjmę więc tylko powierzchnię trzech ścian zewnętrznych, przez które ucieka ciepło na zewnątrz. Ścianę wspólna z sąsiadem pominę, zakładając że przez nią ciepło nie ucieka, bo sąsiad mieszka i grzeje. Należy pamiętać, by od powierzchni ścian odjąć powierzchnię okien, które uwzględniliśmy już wcześniej.
Powierzchnia ścian po odjęciu powierzchni okien: S = 90 – 13,5 = 76,5 m2
Współczynnik przenikania ciepła dla ścian: U = 0,25 W/(m2*K)
q = U * S = 0,25 * 76,5 = 19,125 [W/K]
Podłoga i sufit
Mieszkanie jest na 1 piętrze. Na górze i na dole mieszka sąsiad, więc można przyjąć, że ciepło przez podłogę i sufit nie ucieka.
q = 0 [W/K]
Obliczyliśmy już straty dla wszystkich elementów.
Sumujemy teraz strumienie składowe, aby obliczyć łączny strumień jednostkowy:
q = 17,55 + 0 + 19,125 + 0 = 36,675 [W/K]
czyli na każdy stopień różnicy temperatur z mieszkania ucieka w przybliżeniu 36,7 watów.
Nadeszła wreszcie pora by wrócić do naszego podstawowego pytania:
Czy warto zatem wyłączać ogrzewanie na noc?
Zakładamy, że temperatura utrzymywana w dzień to 22 stopnie. W nocy zgadzamy się na to, żeby temperatura obniżyła się do 18 stopni, ale nie niżej. Jeżeli spadnie niżej, to powinno włączyć się ogrzewanie i utrzymać 18 stopni.
Temperatura dzienna ma być utrzymywana w godzinach między 6.00 a 23.00, a nocna od 23.00 do 6.00.
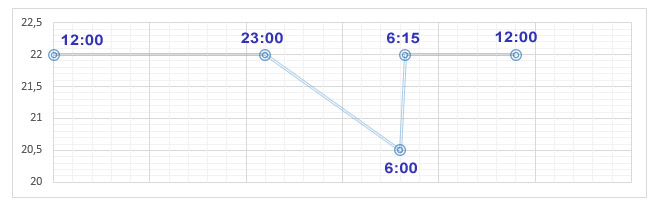
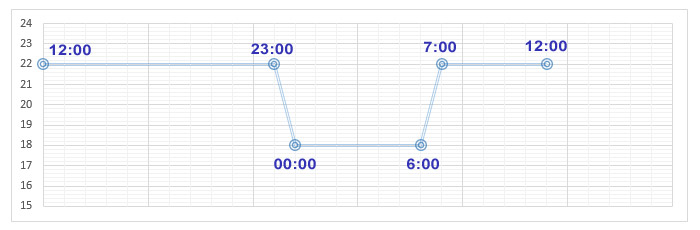
Przyjrzyjmy się jak będzie przebiegał dobowy cykl zmian temperatury.
O godzinie 23.00 wyłączamy ogrzewanie. Mieszkanie zaczyna się w sposób naturalny wychładzać, a temperatura powoli spada. W przedziale od 22 do 18 stopni ogrzewanie się nie włączy. O 6.00 rano włącza się ogrzewanie i podnosi temperaturę do 22 stopni. Taką temperaturę utrzymuje do godziny 23.00. Cykl zaczyna się od początku.
Dokładnie taki eksperyment przeprowadziłem u siebie w domu. Na zewnątrz było wtedy okolicy 0 stopni.
Okazało się, że temperatura spadła w nocy o 1,5 stopnia, do poziomu 20,5 stopnia o godzinie 6.00. Ogrzewanie nie włączyło się więc w nocy ani razu.
O godzinie 6.00 ogrzewanie włączyło się i w ciągu 15 minut nagrzało mieszkanie do temperatury dziennej 22 stopnie.
Przebieg zmian temperatury wyglądał więc tak:
Przeanalizujmy dokładnie co się działo w trakcie całego cyklu.
Jako punkt startu czasu przyjmiemy godzinę 12:00 (w południe). Dla każdego etapu obliczymy energię jaką traci mieszkanie.
Etap 1
12:00 – 23:00 (czas trwania 11 godzin) utrzymywana jest stała temperatura 22 stopnie
Straty energii to:
![]()
gdzie:
q – jednostkowa strata ciepła mieszkania [W/K]
Tw – temperatura wewnątrz mieszkania [K]
Tz – temperatura otoczenia na zewnątrz [K]
t – czas trwania etapu [h]
czyli, energia utracona w pierwszym etapie:
E1 = 36,7 * (22 – 0) * 11 = 36,7 * 22 * 11 = 8 881 [Wh] = 8,881 {kWh]
Etap 2
23:00 – 6:00 (czas trwania 7 godzin) ogrzewanie wyłącza się i mieszkanie zaczyna się powoli wychładzać.
Z mieszkania ucieka energia i temperatura spada. Ogrzewanie się nie włącza, energia nie jest uzupełniana.
Od 23:00 do godziny 6:00 z mieszkania ucieknie pewna ilość energii która oznaczymy –E (minus E). Energię tą będziemy musieli później uzupełnić.
Temperatura spada według krzywej wykładniczej. Ze względu na dużą bezwładność cieplną mieszkania jest to wąski zakres początkowy tej krzywej, gdzie z dużą dokładnością jest ona zbliżona do linii prostej. Można więc śmiało przyjąć, że średnia temperatura jaka panowała w trakcie wychładzania, to średnia arytmetyczna temperatury początkowej i końcowej, czyli:
(22 – 20,5)/2 = 21,25 stopnia
Utrata energii w tym czasie wyniesie więc:
E2 = 36,7 * (21,25 – 0) * 7 = 5 459 [Wh] = 5,459 [kWh]
Etap 3
6:00 – 6:15 (czas trwania 0,25 godziny) ogrzewanie włącza się i w ciągu 15 minut nagrzewa mieszkanie do 22 stopni.
Ogrzewanie, aby podnieść temperaturę do wartości początkowej identycznej jak przed wychłodzeniem, musi uzupełnić utraconą wcześniej energię. Aby uzupełnić utraconą energię ogrzewanie musi dostarczyć do mieszkania taką samą ilość energii (+E) jaka została utracona w czasie wychładzania (-E). Energia stracona (-E) i uzupełniona (+E) są sobie równe, więc ich konkretna wartość jest dla naszego bilansu bez znaczenia, bo w całym procesie ich wartości znoszą się
(-E) + (+E) = 0
Podobnie jak przy wychładzaniu, zmiana temperatury przy podgrzewaniu przebiega w praktycznie liniowym przedziale krzywej wykładniczej, więc średnia temperatura to:
(22 – 20,5)/2 = 21,25 stopnia
Utrata energii w tym czasie wyniesie więc:
E3 = 36,7 * (21,25 – 0) * 0,25 = 195 [Wh] = 0,195 [kWh]
Etap 4
6:15 – 12:00 (czas trwania 5,75 godziny) utrzymywana jest stała temperatura 22 stopnie
W tym czasie z mieszkania ucieka:
E4 = 36,7 * (22 – 0) * 5,75 = 4 643 [Wh] = 4,642 [kWh]
Bilans strat ciepła
Aby obliczyć łączne straty ciepła z całej doby musimy oczywiście zsumować straty z wszystkich czterech etapów.
Czyli:
E = E2 + E2 + E3 + E4 = 8,881 + 5,459 + 0,195 + 4,642 = 19,177 [kWh]
W czasie pełnego cyklu z wyłączaniem ogrzewania na noc, w ciągu jednej doby moje mieszkanie zużyło 19,177 kWh energii.
Ile energii zużyłoby mieszkanie gdybym nie wyłączył ogrzewania na noc?
Cykl jest prosty. Czas cyklu to 24 godziny. Temperatura 22 stopnie przez cały czas trwania cyklu.
Stracona energia:
E = 36,7 * (22 – 0) * 24 = 19 378 [Wh] = 19,378 [kWh]
Ile zaoszczędziłem?
Różnica energii między cyklem z wyłączaniem ogrzewania a cyklem bez wyłączania ogrzewania to:
19,378 – 19,177 = 0,201 [kWh]
W ciągu doby oszczędzam więc 0,201 kWh.
W ciągu miesiąca będzie to: 30 * 0,201 = 6 [kWh]
Zakładając że w ciągu roku ogrzewanie działa przez 5 miesięcy, to w roku oszczędzam: 5 * 6 = 30 kWh energii.
Koszt 1 kWh energii przy posiadanym przeze mnie ogrzewaniu gazowym to 0,31 PLN.
W ciągu roku oszczędzam więc na wyłączaniu ogrzewania na noc: 30 * 0,31 = 9,3 PLN (!!!) 🙂
9 złotych i 30 groszy rocznie
Tyle zaoszczędzę na wyłączaniu ogrzewania. Mówiąc szczerze … słabo.
Montując sterownik ogrzewania, intuicyjnie zakładałem (niczego wtedy nie licząc) że oszczędności będą większe. Szczegółowa analiza nie pozostawia jednak wątpliwości. Szału nie ma.
Ale, ale … nie ma co popadać w pesymizm! Wniosek powinien być inny! Zdecydowanie bardziej pozytywny!
Moje mieszkanie, jest zbudowane z dobrych materiałów i po prostu nie traci zbyt wiele ciepła. Wyłączanie ogrzewania na noc nie przynosi więc takich oszczędności, jak do tej pory myślałem, bo temperatura w ciągu nocy niewiele się obniża. Jednocześnie oznacza to, że ze względu na małe straty ciepła, koszt ogrzewania mojego mieszkania jest relatywnie niski. Nie traci ono zbyt wiele ciepła, więc kaloryfery włączają się na krótko, zaledwie kilka razy na dobę.
Zakup i montaż skomplikowanych regulatorów za kilkaset złotych, w moim przypadku zupełnie mija się z celem.
Kiedy wyłączanie ogrzewania na noc się opłaca?
Wyobraźmy obie nieco starszy budynek. Budowany według starszej technologii, słabiej ocieplony, szybciej tracący energię. Wcale nie trzeba cofać się daleko. Wystarczy przed 2014 rok, kiedy wymagania nie były jeszcze tak wysokie. Można do tego dołożyć gorszą jakość okien i jakieś nieszczelności. Jednym słowem, załóżmy, że mieszkamy w mieszkaniu, które szybciej traci ciepło.
Załóżmy więc, że:
– temperatura dzienna to 22 stopnie
– temperatura nocna to 18 stopni
– temperatura zewnętrzna -5 stopni
– przy wychładzaniu ogrzewania wieczorem temperatura w mieszkaniu spada z 22 do 18 stopni w ciągu 1 godziny
– przy ogrzewaniu mieszkania rano, temperatura w mieszkaniu rośnie z 18 do 22 stopni w ciągu 1 godziny
– jednostkowe straty ciepła w mieszkaniu wynoszą q = 200 [W/K]
Przebieg zmian temperatury wyglądał tak:
Policzmy straty w czasie całego cyklu.
Etap 1 – dzień
12:00 do 23:00 (czas trwania 11 godzin)
Stracona energia:
E1 = 200 * (22- (-5)) * 11 = 200 * 27 * 11 = 59 400 [Wh] = 59,4 {kWh]
Etap 2 – schładzanie
23:00 do 0:00 (czas trwania 1 godzina)
średnia temperatura w czasie schładzania (22-18)/2 = 20 stopni
Stracona energia:
E2 = 200 * (20 –(-5)) * 1 = 5000 [Wh] = 5 [kWh]
Etap 3 – noc
0:00 do 6:00 (czas trwania 6 godzin)
Stracona energia:
E3 = 200 * (18-(-5)) * 6 = 27 600 [Wh] = 27,6 [kWh]
Etap 4 – podgrzewanie
6:00 do 7:00 (czas trwania 1 godzina)
średnia temperatura w czasie schładzania (22-18)/2 = 20 stopni
Stracona energia:
E4 = 200 * (20 –(-5)) * 1 = 5000 [Wh] = 5 [kWh]
Etap 5 – dzień
7:00 – 12:00 (czas trwania 5 godzin)
Stracona energia:
E5 = 200 * (22-(-5)) * 5 = 27 000 [Wh] = 27 [kWh]
Łączne straty energii w ciągu całego cyklu:
E = E1 + E2 + E3 + E4 + E5 = 59,4 + 5 + 27,6 + 5 + 27 = 124 [kWh]
Straty bez wyłączania ogrzewania na noc:
E = 200 * (22-(-5)) *24 = 129,6 [kWh]
Oszczędność w czasie jednej doby to:
129,6 – 124 = 5,6 [kWh]
miesięcznie:
5,6 * 30 = 168 [kWh]
co daje:
– przy ogrzewaniu gazem
168 * 0,31 = 52,08 PLN oszczędności miesięcznie
52,08 * 5 = 264 PLN oszczędności rocznie
– przy ogrzewaniu prądem
169 * 0,58 = 98,02 PLN oszczędności miesięcznie
98,02 * 5 = 490 PLN oszczędności rocznie
Tutaj wartości są już bardziej interesujące. Widać od razu, że przy nieco gorszych parametrach cieplnych mieszkania, czyli relatywnie większych jednostkowych stratach ciepła, kwoty możliwe do zaoszczędzenia, przez obniżanie temperatury na noc, stają się interesujące.
Warto zauważyć, że jednostkowe straty ciepła zależą nie tylko od właściwości izolacyjnych mieszkania (U), ale dokładnie w takim samym stopniu od powierzchni (S) ścian bocznych graniczących z otoczeniem zewnętrznym oraz powierzchni podłogi i sufitu.
Dla przypomnienia, jednostkowy strumień ciepła to iloczyn tych dwóch wielkości:
Może się wiec okazać, że pomimo tego że mamy doskonale ocieplone mieszkanie, to jego duża powierzania sprawi, że straty ciepła będą na tyle duże, że obniżanie temperatury na noc będzie miało wymierny sens. Obrazowo mówiąc, iloczyn 10 * 1 da taki sam wynik co iloczyn 1 * 10, czyli małe straty ciepła przy dużej powierzchni mogą dać taki sam wynik, jak duże straty ciepła, przy małej powierzchni.
Gdzie powstały oszczędności?
Warto zastanowić się, gdzie w całym tym procesie powstają oszczędności, które udało nam się obliczyć? Spoglądając na cały proces łatwo zauważyć, że oszczędności powstają wyłącznie w czasie, gdy średnia temperatura jaka utrzymywana jest w mieszkaniu jest niższa niż temperatura dzienna.
Jeżeli temperatura dzienna to 22 stopnie, a w nocy to np. 20 stopni, to w czasie nocy straty energii z naszego mieszkania są mniejsze, proporcjonalnie do różnicy tych temperatur (2 stopnie). Wracając do początku tego artykułu wiemy, że jednostkowa utrata ciepła (q), mówi nam o tym ile ciepła ucieka na każdy 1 stopień różnicy temperatur. Stąd bierze się nasza oszczędność. Obniżenie temperatury na noc o 2 stopnie, oznacza że w tym czasie będziemy tracili o 2 * q mniej ciepła.
Do tego dochodzą oszczędności na średniej temperaturze w czasie trwania stanów przejściowych (wychładzanie wieczorem i nagrzewanie rano). Średnią temperaturę w tym czasie można przyjąć jako średnią arytmetyczną temperatury początkowej i końcowej.
Czy da się to obliczyć jeszcze prościej?
Tak. Da się.
Oczywiście uproszczenie obliczeń odbywa się kosztem ich dokładności, ale w większości przypadków pozwoli to szybko oszacować czy warto bardziej precyzyjnie zając się tematem.
Uproszczenie opiera się na założeniu, że w stanach przejściowych (wychładzaniu i podgrzewaniu) powstające oszczędności nie są znaczące, a główne oszczędności powstają w czasie, gdy panuje obniżona temperatura. Wystarczy więc policzyć oszczędności jakie powstają w tym czasie. Otrzymamy w ten sposób wynik będzie zawsze nieco zaniżony, co oznacza, że ostateczne oszczędności będą większe.
Jeżeli więc przy tym prostym szacunku wyjdą warte uwagi wartości, to oznacza, że warto policzyć wszystko dokładniej, według przedstawionego przeze mnie wcześniej schematu.
Do obliczeń potrzebna nam będzie jednostkowa strata ciepłą w naszym mieszkaniu oraz różnica temperatury pomiędzy temperaturą utrzymywaną na stałe w dzień, a temperaturą obniżoną w nocy.
Wróćmy więc do poprzedniego przykładu, w którym przyjęliśmy, że jednostkowe straty ciepła w mieszkaniu wynoszą q = 200 [W/K], a temperaturę na noc obniżamy o T = 4 stopnie, w czasie t = 6 godzin (w godzinach 0:00 do 6:00).
Zaoszczędzona w tym czasie energia to:
podstawiamy wartości:
E = 200 * 4 * 6 = 4800 [Wh] = 4,8 [kWh]
według przybliżonych szacunków, ciągu jednej doby oszczędzamy 4,8 [kWh]
roczna oszczędność (5 miesięcy, 30 dni w miesiącu):
5 * 30 * 4,8 = 720 [kWh}
roczna oszczędność na gazie (cena gazu 0,31 PLN/kWh):
720 * 0,31 = 223,20 PLN
roczna oszczędność na prądzie (cena prądu 0,58 PLN/kWh):
720 * 0,58 = 417,60 PLN
Widać że szacowanie tych wartości działa przyzwoicie, ale zaniża w tym przypadku wynik o mniej więcej 15%.
Podsumujmy nasze spostrzeżenia
W średniej wielkości mieszkaniu (50 – 80 m2) wybudowanym po 2014 roku, ze względu na obowiązujące wymagania dotyczące współczynnika przenikania ciepła, straty ciepła są niskie. Obniżanie temperatury na noc może być nieuzasadnione ekonomicznie. W moim przypadku oszczędności wynoszą około 9 PLN rocznie. Koszt zakupu prostego sterownika ogrzewania np. typu AURATON 2025 to około 120 PLN. Oznacza to, że sam sterownik będzie zwracał się ponad 13 lat.
Żeby ocenić opłacalność obniżania temperatury na noc, należy policzyć jednostkową utratę ciepła dla naszego mieszkania, czyli ilość ciepła jaka ucieka z naszego mieszkania na każdy stopień różnicy temperatur pomiędzy wnętrem mieszkania a otoczeniem. Jeżeli jednostkowy strumień ciepła q > 50 [W/K] to warto przeprowadzić obliczenia i analizę według zawartych w artykule wskazówek.
Jednostkowy strumień ciepła uciekającego z mieszkania zależy od dwóch parametrów w identycznym stopniu.
Pierwszy z nich to współczynnik przenikania ciepła (U). Im wyższy, tym gorzej. Dla mieszkań wybudowanych przed 2014 rokiem, może on mieć wysokie wartość, że względu na to, że wymagania budowlane były wtedy znacznie słabsze. Można przyjąć że im starszy budynek, tym wyższy to współczynnik przenikania ciepła i co za tym idzie, wyższe straty ciepła. Jeżeli mieszkasz mieszkaniu wybudowanym przed 2014 rokiem, wykonaj obliczenia.
Drugi parametr to powierzchnia ścian, okien, podłogi, sufitu, drzwi zewnętrznych, przez które ucieka ciepła. Im większa jest ich łączna powierzchnia, tym większe straty. Przy bardzo dużych mieszkaniach, oraz w zasadzie wszystkich domach, ten parametr sprawia, że jednostkowe straty ciepła mogą być duże, pomimo zastosowania wysokiej jakości materiałów izolacyjnych i obniżanie temperatury najczęściej jest uzasadnione, przynosząc oszczędności na poziomie kilkuset złotych rocznie. W tych przypadkach zalecam wykonanie obliczeń. To nic nie kosztuje.
Dla nowego domu o powierzchni 200m2 wybudowanego po 2014 jednostkowy strumień traconego ciepła na poziomie 150 W/K nie jest niczym niezwykłym. Obniżenie temperatury na noc o 4 stopnie przy tanim ogrzewaniu gazowym, przyniesie w takim domu oszczędności na poziomie 200 PLN rocznie.
a teraz ZRÓB COŚ DLA MNIE!
Blog żyje z odwiedzin. Jeżeli przydał Ci się raz, to jest duża szansa, że przyda Ci się kiedyś jeszcze. Oceń proszę artykuł, polub go, albo jeszcze lepiej udostępnij znajomym, np. na Facebooku. To dla mnie ważne! Odpowiednie przyciski znajdziesz poniżej.
Jeżeli zrewanżujesz mi się tym właśnie, a do tego zostawisz komentarz pod artykułem, to będę zadowolony.
Dzięki!
Jacek

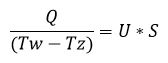
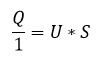
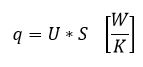





Fajny artykuł – nurtuje mnie jeszcze inne pytanie
wyjeżdżam na weekend – czy jest sens zredukować temperaturę do np. 7 stopni przeciwzamarzaniowych
czy lepiej utrzymywać wyższą „zredukowaną”? np 16?
redukcja do 7 stopni spowoduje wychłodzenie ścian, które mają duuuużą pojemność cieplną. Ponowne nagrzanie będzie trwało długo i w tym czasie pomimo że temperatura powietrza w mieszkaniu wróci np. do 22 stopni, to ściany będą zimne i będziesz odczuwał dyskomfort cieplny do czasu aż nagrzeją się również ściany … mówiąc obrazowo ściany będą jakby promieniowały chłodem. Jeżeli przez pewien czas jesteś w stanie taki dyskomfort zaakceptować, to OK. Jeżeli natomiast masz małe dziecko, które w tym mieszkaniu będziesz np. kąpał wieczorem, to nie zalecam obniżania do 7 stopni.
Ściany nie są w stanie odbierać calego ciepła z powietrza i cieplo bardziej ucieka wentylacją. Dlatego dla mnie wątpliwe jest czy zaoszczedzisz nawet te 9 zlotych rocznie. Podobno lepiej jest grzać non stop delikatnie niz „nadrabiać” pozniej. Taką opinię podają rozne zrodla.
Nie chodzi o to, by grzać non-stop, ale o to, by stale utrzymywać odpowiednią dla siebie temperaturę. W dobrze ocieplonym budynku grzejniki, by utrzymać założoną temperaturę nie grzeją non-stop, tylko kilka razy na dobę włączają się na krótką chwilę.
Można ewentualnie pomyśleć nad lekkim obniżeniem temperatury na noc, ale nie z powodu oszczędności, a ze zwykłego komfortu … w chłodniejszym lepiej się śpi.
Przyjęty w rozważaniach model uwzględnia utratę ciepła przez m.in przez wentylację, ponieważ spadek temperatury przy obniżeniu nocnym następuje na skutek ucieczki ciepła wszystkimi kanałami, a nie tylko przez ściany.
Przy słabo ocieplonych budynkach, zabieg obniżenia temperatury może się opłacać.
Warto też uwzględnić to, że im wyższa temperatura tym ciepło szybciej ucieka (herbata najszybciej stygnie gdy jest gorąca według krzywej wykładniczej https://pl.wikipedia.org/wiki/Prawo_stygnięcia). Zatem im większa różnica temperatur pomiędzy wnętrzem pomieszczenia a otoczeniem tym szybciej ciepło ucieka. Uważam więc, że obniżanie temp. na noc albo po wyjściu z domu do pracy ma sens. Zmniejsza się wtedy gradient i straty maleją. Temperaturę powinno się podwyższać wtedy gdy korzystamy z pomieszczenia biorąc pod uwagę jego bezwładność cieplną – podwyższamy temp. np. na 2 godz. przed powrotem z pracy i obniżamy na 2 godz. przed snem. Ciekawy artykuł i daje do myślenia.
Pozdrawiam Wojtek 🙂
Przy różnicy temperatur na poziomie kilku – kilkunastu stopni (gdy na zewnątrz zamiast 0 będzie np. -15 stopni), oraz bardzo długiej stałej czasowej mieszkania (u mnie, z tego co pamiętam z obliczeń, to około 90 godzin), zjawisko o którym piszesz możliwe, że będzie miało wpływ na dziesiąte miejsce po przecinku. Mówiąc obrazowo: szklanka ma tysiące razy krótszą stałą czasową (czyli tysiące razy razy szybciej stygnie), a mieszkania zwykle nie nagrzewany do 100 stopni Celsjusza, wiec startowa różnica temperatur nigdy nie osiągnie takiej wartości o jakiej wspominasz. Rozpatrywanie takiego przypadku, na potrzeby artykułu o ogrzewaniu mieszkania, jest bardzo ciekawe, ale nie wnosi nic do sprawy.
Pozdrawiam
Jacek
Dlaczego temperatura na zewnątrz jest stała? Wnioski będą te same, ale wyjdą trochę wyższe oszczędności.
Michał,
Przyjmujemy stałą temperaturę, żeby było łatwiej liczyć.
Jeżeli temperatura była by zmienna to musielibyśmy znać przebieg jej zmienności w czasie. Następnie ten przebieg opisać wielomianem n-tego stopnia za pomocą jednej z matematycznych metod interpolacji, aproksymacji, estymacji. Zbadać czy wielomian nie zawiera osobliwości w interesującym nas przedziale. Następnie prawo stygnięcia Newton’a zmodyfikować, by punkt temperatury końcowej był uzależniony w czasie, zgodnie z wielomianem opisującym jej przebieg, a następne stosując najlepiej przekształcenie Laplace’a i rachunek różniczkowo-całkowy wykonać obliczenia. Trochę roboty jest i nie sądzę by różnica (raczej na poziomie pierwszego miejsca po przecinku) była aż tak istotna.
Myślę, że możesz spróbować to policzyć i wrzucić wyniki poniżej w komentarzu. Sam chętnie zobaczę o ile zmienią się obliczone oszczędności.
Zrobiłem trochę inaczej. Temperatury zewnętrzne wziąłem z zapisów stacji meteo. Po postawieniu danych (odczyty temp. co dwie godziny) wyszła oszczędność 332 W/doba, dla mieszkania ze stratą 36,7. I to tylko dlatego, że było ochłodzenie i temp. zew. nie wróciła do +2 stopni tylko utrzymała na -2.
Liczyłem na większe dobowe różnice temperatur.
Trochę pracy włożyłeś, ale przynajmniej masz teraz jasność w temacie.
Pozdrawiam!
Witam.
Jestem laikiem w sprawach fizyki. Analizując treść artykułów mam następujące pytania:
– czy na podstawie różnicy temperatur wewnętrznych i zewnętrznych przy czasowym, np.5 godz., wyłączonym ogrzewaniu można obliczyć przybliżony współczynnik strat ciepła dla danego pomieszczenia. Pytanie wynika z trudności jego oszacowania w sytuacji budynków z lat siedemdziesiątych docieplanych, z wymienionymi oknami itd. Jeżeli moje przypuszczenie jest prawdziwe prosiłbym o komentarz, wskazówki.
Pozdrawiam.
Henryk,
Wykonując eksperyment jaki opisałeś wyznaczysz stałą czasową mieszkania. Aby wyznaczyć w przybliżeniu średni współczynnik strat dla całego mieszkania musisz zrobić inaczej.
1. Ustal jaka jest różnica temperatur pomiędzy wnętrzem mieszkania a otoczeniem w czasie trwania eksperymentu.
2. Ogrzewaj mieszkanie normalnie, tak by temperatura wewnątrz była stała przez cały czas eksperymentu !!!
3. Odczytaj wskazania liczników energii (ciepła, prądu, gazu) na początku eksperymentu i na końcu eksperymentu. Przelicz wszystko na kWh. Zsumuj ilość energii zużytej w czasie eksperymentu (nawet jeżeli np. nie masz ogrzewania elektrycznego, to energia cieplna z urządzeń pracujących w domu i tak w formie ciepła jest przez nie emitowana). Suma tej energii to będzie Q (we wzorze poniżej). Chodzi o to, żeby obliczyć ile ciepła musiałeś dostarczyć w czasie trwania eksperymentu, żeby utrzymać stałą temperaturę.
4. Oblicz „U” średni współczynnik przenikania ciepła dla Twojego mieszkania z zależności:
U = Q / [t * S * (Tw – Tz)]
gdzie:
Q – suma energii z liczników [kWh]
t – czas trwania eksperymentu [h]
S – powierzchnia ścian graniczących z otoczeniem razem z drzwiami i oknami (jeżeli nad i pod Tobą nie ma sąsiada tylko ziemia lub dach to odpowiednio doliczasz podłogę i/lub sufit)
Tw – temperatura wewnątrz
Tz – temperatura na zewnątrz
i to tyle.
Pozdrawiam
Bardzo przydatny artykuł głowiliśmy sie z małżonka od jakiegos czasu i super ze sie natknęliśmy , pozdrawiamy
Witam.
Mieszkam w 30 letnim domu wyremontowanym i docieplonym 15 cm styropianem. Wymieniłem okna na plastykowe z potrójnymi szybami. Na parterze posadzki też dociepliłem podobnej grubości styropianem. Interesują mnie straty ciepła w ciągu roku w przeliczeniu na m2. Czy szacunkowo mógłbyś podać?
Drugi interesujący mnie temat, nawiązujący do powyższego artykułu, dotyczy obniżenia temperatury w pomieszczeniach w celu oszczędności ciepła. Moje ściany mają dużą akumulację i krótkotrwałe zmiany temperatury na niewiele się zdadzą. Wyobrażam sobie obniżenie temperatury do 18 st. lub poniżej i taką utrzymywać w przeciągu całej doby. Oczywiście Trudno siedzieć w fotelu i oglądać TV, lub czytać, w temp 16 stopni, bo po chwili zacznie się marznąć, a mój komfort cieplny to 23 stopnie. Żona lubi jeszcze cieplej i czasem uruchamia farelkę, ze szkodą dla budżetu domowego. Przyszedł mi więc pomysł, żeby dogrzewać wyznaczone miejsce, ale farelką zasilaną ciepłą wodą z co. W handlu są dostępne nagrzewnice wodne z inteligentnym sterowaniem i można podłączyć ją elastycznymi wężami tak, żeby nagrzewnicę móc ustawiać w dowolnym miejscu.
Dodam, że dom posiada duży salon i on stanowi większość powierzchni całkowitej, dlatego takie dogrzewanie byłoby sensowne. Grzanie miejscowe jest znane od dawna, lecz w pomieszczeniach zawodowych i mam wątpliwości czy w mieszkaniu będzie dobre
W Twoim zapytaniu jest za mało danych by to policzyć.
Szczegółowy przepis na samodzielne policzenie tego znajdziesz w artykule: Jak policzyć straty ciepła uciekającego z mieszkania przez ściany, okna, drzwi, podłogę, strop, dach?
Jeżeli chodzi o sprawę nr 2, to obniżenie temperatury ścian do 18 stopni spowoduje obniżenie tzw. wrażenia komfortu cieplnego i lokalne dogrzewanie nie przyniesie satysfakcjonującego efektu …
Więcej na ten temat znajdziesz, gdy poszukasz informacji na temat: wykres Koniga.
Nie zmieściło się w poprzednim mailu.
Cd.
Czy mógłbyś oszacować oszczędności wynikające z takiego rozwiązania?
Z góry dziękuję i z zaciekawieniem czytam Twoje artykuły.
Pozdrawiam.
Zdzisław.
Takie oszczędności szacowałem już w artykule: Ile zaoszczędzisz na ogrzewaniu, obniżając o 1 stopień temperaturę w mieszkaniu lub domu? [KALKULACJA]
A ja znam taki przykład – dom typu bliźniak, mieszkają 2 rodzimy. Po lewej kobieta z trójką dzieci, grzeje non stop na 24 stopnie. Po prawej oszczędni Państwo, zmniejszają temperaturę na noc i kiedy tylko się jeszcze da. Ona płaci 2000zł rocznie oni 2600zł. Oni chodzą po domu w krótkim rękawku a ci drudzy całą zimę w swetrach.
A w tych wszystkich wyliczeniach nie wzięto pod uwagę kosztów leczenia.
Z własnego podwórka: moi rodzice nie przekraczali nigdy 18 stopni w zimie. Mama co chwila chora. Na leki wydała przynajmniej 2x więcej niż zaoszczędziła na ogrzewaniu.
Sprostowanie do poprzedniego postu: Pani z dziećmi płaci 2000 zł, a Państwo Oszczędni 2600zł.
Wow w 15 minut jesteś w stanie podgrzać o 1,5C? Mówimy tu o jakiejś kawalerce? Czy masz termometr przy samym grzejniku? A może masz ogrzewanie podłogowe i nowoczesne budownictwo?
Jeżeli jest faktycznie zimno, to u mnie podgrzanie mieszkania o 0,5C to jest dobra godzina (mówimy o częściowo ocieplonym mieszkaniu 95m2 w kamienicy na najwyższym piętrze – nade mną jest strych w którym utrzymuje się średnio 1-4C). Ostatnio gdy nie miałem prądu przez 3 godziny, temperatura spadła o 1C, to ponowne podgrzanie zajęło ponad 2h w trakcie których piec dobijał do maksymalnej roboczej temperatury (65C szło w grzejniki, aż parzyły).
Zeszłej zimy robiłem takie eksperymenty, ale ostatecznie zdecydowałem się utrzymywać cały czas 21C, właśnie ze względu na długą pracę pieca w maksymalnych warunkach.
Jest jeszcze jeden aspekt, który może sprawić, że praktyka będzie się mocno rozmijała z teorią – maksymalna moc jaką jesteśmy w stanie dostarczyć do mieszkania vs moc którą tracimy. Jeśli te moce są podobne, a tak u mnie się dzieje przy mrozach powyżej -10C, to te obliczenia nie mają sensu. Np. przy -16C żeby nie wiem ile chodził piec, nigdy nie uzyskam 21C w mieszkaniu. Muszę przestawiać na 20 lub 20,5C, co jest na granicy. Zmniejszanie temp na noc np. na 18 czy 19C nie ma najmniejszego sensu – mieszkanie stygnie w takich warunkach bardzo szybko, a ponowne nagrzanie do 20C trwa naprawdę długo (piec chodzi wtedy non stop).
nie podano temeperatury wody grzewczej ktora dogrzewa w ciagu godziny pomieszczenia z temp 18 na 22 stopnie w pomieszczeniach.To jest bardzo interesujace jaka musi byc temeperatura wody grzewczej przy temp na zwenatrz 0 stopni.